Mathaíno perissótera.

Learn more.

A lifelong motto.

Mathaíno = I learn.  μάθημα (máthema) = a learned thing.  Mathemata are “learned things.”  This word is at the root of the word “mathematics.”

Mathematics and reckoning (numbers, arithmetic) are not the same.

Troy, for example, the town that lay between two continents, Europe and Asia, right in the strait that leads into the Black Sea, has a mathematical design.

Many turf mazes in England were named Troy Town, Troy-town or variations on that theme  presumably because, in popular legend, the walls of the city of Troy were constructed in such a confusing and complex way that any enemy who entered them would be unable to find his way out.

Welsh hilltop turf mazes (none of which now exist) were called Caerdroia, which can be translated as “City of Troy” (or perhaps “castle of turns”).

The name “Troy” has been associated with labyrinths from ancient times. An Etruscan terracotta wine-jar from Tragliatella, Italy, shows a seven-ring labyrinth marked with the word TRUIA (which may refer to Troy). To its left, two armed soldiers appear to be riding out of the labyrinth on horseback, while on the right two couples are shown copulating. The vase dates from about 630 BCE.

Of the eight surviving historic turf mazes in England, three have “Troy” names. “The City of Troy” is a small but well-maintained roadside maze near the small villages of Dalby, Brandsby, and Skewsby, not far from Sheriff Hutton in the Howardian Hills of North Yorkshire.

“Troy”, a beautiful maze in a private garden at Troy Farm, Somerton, Oxfordshire, is rather larger, and “Troy Town” maze on St Agnes, the Isles of Scilly, is a small maze of turf and small stones and is reputed to have been laid down in 1729 by the son of a local lighthouse keeper.

All three follow the classical labyrinth pattern (as found on coins from ancient Knossos) rather than the medieval variation.

This  Troy design may be the oldest town planning scheme that we know. Even older than Jericho.

This Troy design is a mathematical scheme.

There is a range of views even among mathematicians and philosophers as to the exact scope and definition of mathematics.

Galileo Galilei (1564–1642) said, “The universe cannot be read until we have learned the language and become familiar with the characters in which it is written. It is written in mathematical language, and the letters are triangles, circles and other geometrical figures, without which means it is humanly impossible to comprehend a single word. Without these, one is wandering about in a dark labyrinth.”

Richard Feynman made the same point:  When nature speaks to us, she uses the language of mathematics.

Carl Friedrich Gauss (1777–1855) referred to mathematics as “the Queen of the Sciences,””

Albert Einstein (1879–1955) stated that “as far as the laws of mathematics refer to reality, they are not certain; and as far as they are certain, they do not refer to reality.”

The most ancient mathematical texts are Plimpton 322 (Babylonian mathematics c. 1900 BCE), the Rhind mathematical papyrus (Egyptian mathematics c. 2000-1800 BCE) and the Moscow mathematical papyrus (Egyptian mathematics c. 1890 BCE).

All of these texts concern the so-called Pythagorean theorem which seems to be the most ancient and widespread mathematical development after basic arithmetic and geometry. This theorem existed long before Pythagoras himself did. The Chinese and Egyptians knew it.

The study of mathematics begins in the 6th century BCE with the Pythagoreans who coined the term “mathematics” from the ancient Greek μάθημα (mathema), meaning “subject of instruction.”  Note that μάθημα is from the same root as “mathaino perissotera,” (I Learn More) the title of this writing.

Greek mathematics refined the methods (especially through the introduction of deductive reasoning and mathematical rigor in proofs) and expanded the subject matter of mathematics.

Chinese mathematics made very early contributions, including a place value system.

The Hindu-Arabic numerical system and the rules for the use of its operations, in use throughout the world today, likely evolved over the course of the first millennium CE in India and was transmitted to the west via Islamic mathematics.

Islamic mathematics developed and expanded the mathematics known to these civilizations.

Many Greek and Arabic texts on mathematics were then translated into Latin which led to further development of mathematics in medieval Europe.

From ancient times through the middle ages spurts of mathematical creativity were often followed by centuries of stagnation.

In 16th century Renaissance Italy, new mathematical developments, interacting with new scientific discoveries, were made at an accelerating pace that continues to the present day.

The origins of mathematical thought lie in the concepts of number, magnitude and form.

Modern studies of animal cognition have shown that these concepts are not unique to humans.

Such concepts would have been part of everyday life in hunter-gatherer societies.

The idea of the “number” concept evolving gradually over time is supported by the existence of languages which preserve the distinction between “one”, “two”, and “many”, but not of numbers larger than two.

The oldest known possibly mathematical object is the Lebombo bone discovered in the Lebombo mountains of Swaziland and dated to approximately 35,000 BC.

The bone consists of 29 distinct notches cut into a baboon’s fibula.

Also prehistoric artifacts discovered in Africa and France dated between 35,000 and 20,000 years old, suggest early attempts to quantify time.

The Ishangi bone, found near the headwaters of the Nile river (northeastern Congo), may be as much as 20,000 years old and consists of a series of tally marks carved in three columns running the length of the bone.

It is thought that the Ishango bone shows either the earliest known demonstration of sequences of prime numbers or a six-month lunar calendar.

Peter Rudman argues in How Mathematics Happened: The First 50,000 Years,  that the development of the concept of prime numbers could only have come about after the concept of division, which he dates to after 10,000 BCE, with prime numbers probably not being understood until about 500 BCE.

Rudman also writes that “no attempt has been made to explain why a tally of something should exhibit multiples of two, prime numbers between 10 and 20, and some numbers that are almost multiples of 10.”

The Ishango bone, according to scholar Alexander Marshack, may have influenced the later development of mathematics in Egypt since, like some entries on the Ishango bone, Egyptian arithmetic also made use of multiplication by 2; this, however, is disputed.

Predynastic Egyptians of the 5th millennium BCE pictorially represented geometric designs.

Megalithic monuments in England and Scotland, dating from the 3rd millennium BCE, incorporate geometric ideas such as circles, ellipses, and Pythagorean triples in their design.

The currently oldest undisputed mathematical usage is in Babylonian and dynastic Egyptian sources.

Thus it took human beings at least 45,000 years from the time when they became more or less like us and used language to develop mathematics as such.

Babylonian mathematics refers to any mathematics of the people of Mesopotamia (modern Iraq) from the days of the early Sumerians through the Hellenistic period and up to the beginning of the Common Era.

The term Babylonian mathematics is used due to the central role of Babylon as the place of study.

During the Arab era, Mesopotamia, especially Baghdad, again became an important center of study for Islamic mathematics.

It’s difficult to find information about Egyptian mathematics, but our knowledge of Babylonian mathematics is derived from more than 400 clay tablets unearthed since the 1850s.

Written in cuneiform, the tablets were inscribed while the clay was moist, and baked hard in an oven or by the heat of the sun.

Some of these tablets appear to be graded homework.

The first evidence of written mathematics dates back to the ancient Sumerians, who built the earliest civilization in Mesopotamia.

The Sumerians developed a complex system of metrology from 3000 BCE.

From around 2500 BCE onwards, the Sumerians wrote multiplication tables on clay tablets and dealt with geometrical exercises and division problems.

The earliest traces of the Babylonian numerals also date back to this period.

Most of the recovered clay tablets date from 1800 to 1600 BCE, and cover topics which include fractions, algebra, quadratic and cubic equations, and the calculation of regular reciprocal pairs.

The tablets also include multiplication tables and methods for solving linear and quadratic equations.

The Babylonian tablet YBC 7289 gives an approximation of √2 accurate to five decimal places.

Babylonian mathematics were written using a sexagesimal (base-60) numeral system.

This is where we get the idea of 60 seconds in a minute, 60 minutes in an hour, and 360 (60 x 6) degrees in a circle, as well as the use of seconds and minutes of arc to denote fractions of a degree.

Babylonian advances in mathematics were facilitated by the fact that 60 has many divisors.

Unlike the Egyptians, Greeks, and Romans, the Babylonians had a true place-value system, where digits written in the left column represented larger values, much as in the decimal system.

The Babylonians had a place-value system, yes, but no kind of decimal point, and so the place value of a symbol often had to be inferred from the context.

Seen another way, though, this decimal point drawback is equivalent to the modern-day usage of floating point arithmetic.

Also, the use of base 60 means that any reciprocal of an integer which is a multiple of divisors of 60 necessarily has a finite expansion to the base 60.

(In our arithmetic, only reciprocals of multiples of 2 and 5 have finite decimal expansions.)

This means that there is a strong argument that the arithmetic Old Babylonian style is considerably more sophisticated than that of our current usage.

The interpretation of Plimpton 322 (the Babylonian mathematical text from 1900 BCE) was the source of controversy for many years after its significance in the context of Pythagorean triangles was realized.

Problems involving equal-area subdivision of triangular and trapezoidal fields (with integer length sides) quickly convert into the need to calculate the square root of 2, or to solve the “Pythagorean equation” in integers.

Rather than considering a square as the sum of two squares, you can think of it as a difference of two squares. After division, (c-a)(c+a)= bb becomes the product of two rational numbers giving 1: (c/b-a/b)(c/b+a/b) = 1.

And then you can solve this by looking at a table of reciprocal pairs.

Solutions of the original equation are thus parametrized by the choice of a rational number x, from which Pythagorean-triple right-triangles can easily be constructed by integer-scaling a right-triangle with sides of length 2x, xx-1, xx+1 (but only if you wish to do so).

All Pythagorean triples arise in this way, and the examples provided in Plimpton 322 involve some quite large numbers, by modern standards, such as (4601, 4800, 6649) in decimal notation.

Egyptian mathematics refers to mathematics written in the Egyptian language. During the Hellenistic period, Greek replaced Egyptian as the written language of Egyptian scholars. Mathematical study in Egypt later continued under the Arab empire as part of Islamic mathematics when Arabic became the written language of Egyptian scholars.

The most extensive Egyptian mathematical text is the Rhind papyrus(sometimes also called the Ahmes Papyrus after its author), dated to c. 1650 BCE but likely a copy of an older document from the Middle Kingdom of about 2000-1800 BC.

The Rhind papyrus is an instruction manual for students in arithmetic and geometry.

In addition to giving area formulas and methods for multiplication, division and working with unit fractions, it also contains evidence of other mathematical knowledge, including composite and prime numbers; arithmetic, geometric and harmonic means; and simplistic understandings of both the Sieve of Eratosthenes and perfect number theory (namely, that of the number 6).

The Rhind papyrus also shows how to solve first order linear equations as well as arithmetic and geometric series.

Another significant Egyptian mathematical text is the Moscow papyrus also from the Middle Kingdom period, dated to c. 1890 BCE.

The Moscow papyrus consists of what are today called word problems or story problems, which were apparently intended as entertainment.

One problem is considered to be of particular importance because it gives a method for finding the volume of a frustum: “If you are told: A truncated pyramid of 6 for the vertical height by 4 on the base by 2 on the top. You are to square this 4, result 16. You are to double 4, result 8. You are to square 2, result 4. You are to add the 16, the 8, and the 4, result 28. You are to take one third of 6, result 2. You are to take 28 twice, result 56. See, it is 56. You will find it right.”

Finally, the Berlin papyrus (c. 1300 BCE) shows that ancient Egyptians could solve a second-order algebraic equation.

Greek mathematics refers to mathematics written in the Greek language from the time of Thales of Miletus (~600 BCE) to the closure of the Academy of Athens in 529 CE.

Greek mathematicians lived in cities spread over the entire Eastern Mediterranean, from Italy to North Africa, but were united by culture and language.

Greek mathematics of the period following Alexander the Great is often called Hellenistic mathematics.

Greek mathematics was much more sophisticated than the mathematics that had been developed by earlier cultures.

All surviving records of pre-Greek mathematics show the use of inductive reasoning, that is, repeated observations used to establish rules of thumb.

Greek mathematicians, by contrast, used deductive reasoning. The Greeks used logic to derive conclusions from definitions and axioms, and used mathematical rigor to prove them.

Greek mathematics is thought to have begun with Thales of Miletus (c. 624–c.546 BCE) and Pythagoras of Samos (c. 582–c. 507 BCE).

Although the extent of the influence is disputed, Thales and Pythagoras were probably inspired by Egyptian and Babylonian mathematics.

According to legend, Pythagoras traveled to Egypt to learn mathematics, geometry, and astronomy from Egyptian priests.

Thales used geometry to solve problems such as calculating the height of pyramids and the distance of ships from the shore.

He is also credited with the first use of deductive reasoning applied to geometry, by deriving four corollaries to Thales’ Theorem.

Thales, therefore, has been hailed as the first true mathematician and the first known individual to whom a mathematical discovery has been attributed.

Pythagoras established the Pythagorean school, whose doctrine it was that mathematics ruled the universe and whose motto was “All is number.”

It was the Pythagoreans who coined the term “mathematics”, and with whom the study of mathematics for its own sake begins.

The Pythagoreans are credited with the first proof of the Pythagorean theorem.

The statement of the Pythagorean theorem has a long history and was known to Chinese and Egyptian thinkers.

The Pythagoreans are also credited with the proof of the existence of irrational numbers.

Plato (428/427 BC – 348/347 BCE) is important as an inspiration in the history of mathematics and as a guide.

The Platonic Academy in Athens became the mathematical center of the world in the 4th century BCE, and it was this school that produced leading mathematicians of the day such as Eudoxus of Cnidus.

Plato discussed the foundations of mathematics, clarified some of the definitions (e.g. that of a line as “breadthless length”) and examined the assumptions everyone had up to that point.

The analytic method of reasoning is ascribed to Plato, and a formula for obtaining Pythagorean triples bears his name.

Eudoxus (408–c.355 BCE) developed the method of exhaustion, a precursor of modern integration, and also a theory of ratios that avoided the problem of incommensurable magnitudes

The method of exhaustion allowed the calculations of areas and volumes of curvilinear figures.

The theory of ratios enabled subsequent geometers to make significant advances in geometry.

Aristotle (384—c.322 BCE) contributed significantly to the development of mathematics by laying the foundations of logic, though he made no specific technical mathematical discoveries.

In the 3rd century BCE, the premier center of mathematical education and research was the Museum of Alexandria.

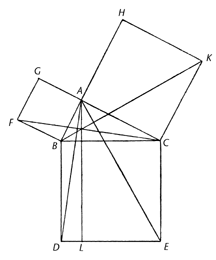
It was in Alexandria that Euclid (c. 300 BCE) taught, and wrote the Elements, widely considered the most successful and influential textbook of all time.

The Elements introduced mathematical rigor through the axiomatic method and is the earliest example of the format still used in mathematics today, that of definition, axiom, theorem, and proof.

Most of the contents of the Elements were already known, but Euclid arranged them into a single, coherent logical framework.

The Elements was known to all educated people in the West until the middle of the 20th century and its contents are still taught in geometry classes today.

I remember this book well.

In addition to teaching the familiar theorems of Euclidean geometry, the Elements was meant as an introductory textbook to all mathematical subjects of the time, such as number theory, algebra and solid geometry, including proofs that the square root of two is irrational and that there are infinitely many prime numbers.

Euclid wrote extensively on other subjects, such as conic sections, optics, spherical geometry, and mechanics, but only half of his writings survive.

The first woman mathematician recorded by history was Hypatia of Alexandria (350 – 415 CE).

Hypatia succeeded her father as the librarian at the great library of Alexandria and wrote many works on applied mathematics.

The “Christian” community in Alexandria punished Hypatia for her intellectual “presumption” by stripping her naked and scraping off her skin with clamshells and roofing tiles.

Archimedes (c.287–212 BCE) of Syracuse, widely considered the greatest mathematician of antiquity, used the method of exhaustion to calculate the area under the arc of a parabola with the summation of an infinite series, in a manner not too dissimilar from modern calculus.

Archimedes also showed one could use the method of exhaustion to calculate the value of π with as much precision as desired, and obtained the most accurate value of π then known, 3¹⁰⁄₇₁ < π < 3¹⁰⁄₇₀.

He also studied the spiral that bears his name, obtained formulas for the volumes of surfaces of revolution (paraboloid, ellipsoid, hyperboloid), and an ingenious system for expressing very large numbers.

While he is also known for his contributions to physics and several advanced mechanical devices, Archimedes himself placed far greater value on the products of his thought and general mathematical principles.

He regarded as his greatest achievement his finding of the surface area and volume of a sphere, which he obtained by proving these are 2/3 the surface area and volume a cylinder circumscribing the sphere.

Apollonius of Perga (c. 262-190 BCE) made significant advances to the study of conic sections, showing that one can obtain all three varieties of conic section by varying the angle of the plane that cuts a double-napped cone.

Apollonius also coined the terminology in use today for conic sections, namely parabola (“place beside” or “comparison”), ellipse (“deficiency”), and hyperbola (“a throw beyond”).

His work Conics is one of the best known and preserved mathematical works from antiquity, and in it he derives many theorems concerning conic sections that would prove invaluable to later mathematicians and astronomers studying planetary motion.

While neither Apollonius nor any other Greek mathematicians made the leap to coordinate geometry, Apollonius’ treatment of curves is in some ways similar to the modern treatment, and some of his work seems to anticipate the development of analytical geometry by René Descartes.

Eratosthenes of Cyrene (c. 276-194 BCE) was the one who devised the Sieve of Eratosthenes for finding prime numbers.

The 3rd century BCE is regarded as the “Golden Age” of Greek mathematics, with advances in pure mathematics henceforth in relative decline.

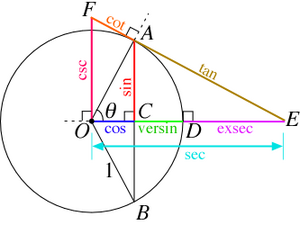
In the centuries that followed, however, significant advances were made in applied mathematics, most notably  in trigonometry to help astronomers.

Hipparchus of Nicaea (c. 190-120 BCE) is considered the founder of trigonometry because he compiled the first known trigonometric table.

He was also the first to use systematically the 360 degree circle.

Heron of Alexandria (c. 10–70 CE) created Heron’s formula for finding the area of a scalene triangle.

Heron also was the first to recognize the possibility of negative numbers possessing square roots.

Menelaus of Alexandria (c. 100 CE) pioneered spherical trigonometry with his Menelaus’ theorem.

The most complete and influential trigonometric work of antiquity is the Almagest of Ptolemy (c. 90-168 CE), a landmark astronomical treatise whose trigonometric tables would be used by astronomers for the next thousand years.

Ptolemy also created Ptolemy’s theorem for deriving trigonometric quantities, and the most accurate value of π (3.1416) outside of China until the medieval period in Europe.

The period between 250 and 350 CE is sometimes referred to as the “Silver Age” of Greek mathematics which had followed a period of stagnation in Greek mathematics.

During this Silver Age,  Diophantus made significant advances in algebra, particularly indterminate analysis which is also known as Diophantine analysis.

The study of Diophantine equations and approximations is a significant area of research to this day.

Diophantus’ main work was the Arithmetica, a collection of 150 algebraic problems dealing with exact solutions to determinate and indeterminate equations.

The Arithmetica had a significant influence on later mathematicians, such as Pierre de Fermat, who arrived at his famous Last theorem after trying to generalize a problem he had read in the Arithmetica (that of dividing a square into two squares).

Diophantus also made significant advances in notation, the Arithmetica being the first instance of algebraic symbolism and syncopation.

Meanwhile in China,  mathematics was so different from that of other parts of the world  it is logical to assume an independent development of the science.

The oldest surviving mathematical text from China is the Chou Pei Suan Ching, variously dated to between 1200 BCE and 100 BCE, though a date of about 300 BCE seems the best guess.

Of particular note is the use in Chinese mathematics of a decimal positional notation system, the so-called “rod numerals” in which distinct ciphers were used for numbers between 1 and 10, and additional ciphers for powers of ten.

This system may have evolved from looking at an abacus.

Thus, the number 123 would be written using the symbol for “1″, followed by the symbol for “100″, then the symbol for “2″ followed by the symbol for “10″, followed by the symbol for “3″.

This was the most advanced number system in the world at the time, in use for several centuries before the common era in Europe and well before the development of the Indian/Arabic numeral system.

Rod numerals allowed the representation of numbers as large as desired and allowed calculations to be carried out on the suan pan or Chinese abacus.

When the suan pan was invented is not certain, but the earliest written mention dates from 190 CE, in Xu Yue’s Supplementary Notes on the Art of Figures.

The oldest Chinese work on geometry is the philosophical Mohist canon c. 330 BCE, compiled by the followers of Mozi (470–390 BCE).

The Mo Jing described various aspects of many fields associated with physical science, and provided a small number of geometrical theorems as well.

In 212 BC, the Emperor Qin Shih Huang (Shi Huang-ti) commanded all books in the Qin Empire other than officially sanctioned ones be burned.

This book burning decree was flouted in some places, but as a consequence of this disastrous decree little is known about ancient Chinese mathematics before this date.

After the babarian book burning of 212 BCE, the Han dynasty (202 BCE–220 CE) produced works of mathematics which presumably expanded on works that lost during the holocaust.

(Notice that the Han period corresponds roughly with the time of the Roman empire in Europe. The Han Chinese are, by far, the largest group in China. They call themselves Han as do other peoples around them. The Japanese word for written characters borrowed from China is kanji which means “Han letter” in Japanese.)

The most important of Han works that expanded on the earlier burned books is The Nine Chapters on the Mathematical Art, the full title of which appeared by 179 CE, but which had existed before under other titles.

The Nine Chapters consists of 246 word problems involving agriculture, business, employment of geometry to figure height spans and dimension ratios for Chinese pagoda towers, engineering and surveying.

Material on right triangles and values of  π is also included.

The Nine Chapters on the Mathematical Art created mathematical proof for the Pythagorean theorem and a mathematical formula for Gaussian elimination.

Lin Hui commented on the work in the 3rd century CE, and gave a value of π accurate to 5 decimal places.

Though more of a matter of computational stamina than theoretical insight, in the 5th century CE Zu Chongzhi computed the value of π to seven decimal places, which remained the most accurate value of π for almost the next 1000 years.

He also established a method which would later be called Cavalieri’s principle to find the volume of a sphere.

The high-water mark of Chinese mathematics occurs in the 13th century (Sung period), with the development of Chinese algebra.

The classic text from the later Sung period is the Precious Mirror of the Four Elements by Chu Shih-chieh (fl. 1280-1303), dealing with the solution of simultaneous higher order algebraic equations similar to Horner’s method.

The Precious Mirror also contains a diagram of Pascal’s triangle with coefficients of binomial expansions through the eighth power, though both appear in Chinese works as early as 1100.

The Chinese also made use of the complex combinatorial diagram known as the magic square and magic circles, described in ancient times and perfected by Yang Hui (1238–1298 CE).

Even after European mathematics began to flourish during the Renaissance, European and Chinese mathematics were separate traditions, with significant Chinese mathematical output in decline from the 13th century onwards.

Jesuit missionaries such as Matteo Ricci carried mathematical ideas back and forth between the two cultures from the 16th to 18th centuries, though at this point far more mathematical ideas were entering China than leaving.

 

On the Indian subcontinent was the Indus Valley civilization that flourished between 2600 and 1900 BCE in the Indus River basin.

The Indus Valley cities were laid out with geometric regularity, but no known mathematical documents survive from this civilization.

The oldest existing mathematical records from India are the Sulba Sutras, dated variously between the 8th century BCE and the 2nd century CE, appendices to religious texts which give simple rules for constructing altars of various shapes, such as squares, rectangles, parallelograms, and others.

This preoccupation with temple functions points to an origin of mathematics in religious ritual, as was perhaps the case in Egypt.

The Sulba Sutras give methods for constructing a circle with approximately the same area as a given square, which implies several different approximations of the value of  π.

In addition, the Sutras compute the square root of 2 to several decimal places, list Pythagorean triples, and give a statement of the Pythagorean theorem.

These were all present in Babylonian science, which would seem to indicate a Mesopotamian influence on Indian mathematics.

It is not known to what extent the Sulba Sutras influenced later Indian mathematicians.

As in China, there is a lack of continuity in Indian mathematics.

Significant advances are separated by long periods of inactivity.

Panini (c. 5th century BCE) formulated the rules for Sanskrit grammar.

His notation was similar to the mathematical notation of today, andhe  used metarules, transformations and recursion.

Pingala (roughly 3rd-1st centuries BCE) in his treatise of prosody uses a device corresponding to a binary numeral system.

His discussion of the combinatrics of meters corresponds to an elementary version of the binomial theorem.

Pingala’s work also contains the basic ideas of Fibonacci numbers, which he called mātrāmeru).

The next significant mathematical documents from India after the Sulba Sutras are the Siddhantas, astronomical treatises from the 4th and 5th centuries CE, the Gupta period, showing strong Hellenistic influence.

They are significant in that they contain the first instance of trigonometric relations based on the half-chord, as is the case in modern trigonometry, rather than the full chord, as was the case in Ptolemaic trigonometry.

Through a series of translation errors, the words “sine” and “cosine” derive from the Sanskrit “jiya” and “kojiya”.

In the 5th century CE, Aryabhata wrote the Aryabhatiya, a slim volume, written in verse, intended to supplement the rules of calculation used in astronomy and mathematical mensuration, though with no feeling for logic or deductive methodology.

Though about half of the entries are wrong, it is in the Aryabhatiya that the decimal place-value system first appears.

Several centuries later, the Muslim mathematician Abu Rihan Biruni described the Aryabhatiya as a “mix of common pebbles and costly crystals”.

In the 7th century, Brahmagupta identified the Brahmagupta theorem, Brahmagupta’s identity, and for the first time, in Brahma sphuta siddhanta he lucidly explained the use of zero as both a placeholder and decimal digit and explained the Hindu Arabic numeral system.

It was from a translation of this Indian text on mathematics (c. 770) that Islamic mathematicians were introduced to this numeral system, which they adapted as Arabic numerals.

Islamic scholars carried knowledge of this number system to Europe by the 12th century, and it has now displaced all older number systems throughout the world.

In the 10th century, Halayudha’s commentary on Pingala’s work contains a study of the Fibonacci sequence and Pascal’s triangle and describes the formation of a matrix.

In the 12th century, Bhaskara II lived in southern India and wrote extensively on mathematics.

His work contains mathematical objects equivalent or approximately equivalent to infinitesimals, derivatives, the mean value theorem and the derivative of the sine function.

To what extent he anticipated the invention of calculus is a controversial subject among historians of mathematics.

In the 14th century, Madhava of Sangamagrama, the founder of the so-called Kerala School of Mathematics, found the Madhava-Leibniz series, and, using 21 terms, computed the value of π as 3.14159265359.

Madhava also found the Madhava-Gregory series to determine the arctangent, the Madhava-Newton power series to determine sine and cosine and the Taylor approximation for sine and cosine functions.

In the 16th century, Jyesthadeva consolidated many of the Kerala School’s developments and theorems in the Yukti-bhāṣā.

However, the Kerala School did not formulate a systematic theory of differentiation and integration, nor is there any direct evidence of their results being transmitted outside Kerala.

Progress in mathematics along with other fields of science stagnated in India with the establishment of Muslim rule in India.

The Islamic empire established across Persia, the Middle East,  Central Asia, North Africa, Iberia and in parts of India in the 8th century made significant contributions towards mathematics.

Although most Islamic texts on mathematics were written in Arabic, most of them were not written by Arabs, since much like the status of Greek in the Hellenistic world, Arabic was used as the written language of non-Arab scholars throughout the Islamic world at the time.

Persians contributed to the world of Mathematics alongside Arabs.

In the 9th century, the Persian mathematician Muhammad ibn Musa al-Khwarismi wrote several important books on the Hindu-Arabic numerals and on methods for solving equations.

His book On the Calculation with Hindu Numerals, written about 825, along with the work of Al-Kindi, were instrumental in spreading Indian mathematics and Indian numerals to the West.

The word algorhythm is derived from the Latinization of his name, Algoritmi, and the word algebra from the title of one of his works,Al-Kitab al-mukhtasar fihisab al-gabr wa’l-mugabala (The Compendious Book on Calculation by Completion and Balancing).

He gave an exhaustive explanation for the algebraic solution of quadratic equations with positive roots, and he was the first to teach algebra in an elementary form and for its own sake.

He also discussed the fundamental method of “reduction” and “balancing”, referring to the transposition of subtracted terms to the other side of an equation, that is, the cancellation of like terms on opposite sides of the equation.

This is the operation which al-Khwārizmī originally described asal-jabr.

His algebra was also no longer concerned “with a series of problems to be resolved, but an exposition which starts with primitive terms in which the combinations must give all possible prototypes for equations, which henceforward explicitly constitute the true object of study.”

He also studied an equation for its own sake and “in a generic manner, insofar as it does not simply emerge in the course of solving a problem, but is specifically called on to define an infinite class of problems.”

Further developments in algebra were made by Al-Karaji in his treatise al-Fakhri, where he extends the methodology to incorporate integer powers and integer roots of unknown quantities.

Something close to a proof by mathematical induction appears in a book written by Al-Karaji around 1000 AD, who used it to prove the binomial theorem, Pascal’s triangle and the sum of integral cubes.

The historian of mathematics, F. Woepcke, praised Al-Karaji for being “the first who introduced the theory of algebraic calculus.”

Also in the 10th century, Abul Wafa translated the works of Diophantus into Arabic.

Ibn al-Haytham was the first mathematician to derive the formula for the sum of the fourth powers, using a method that is readily generalizable for determining the general formula for the sum of any integral powers.

He performed an integration in order to find the volume of a paraboloid, and was able to generalize his result for the integrals of polynomials up to the fourth degree.

So he came quite close to finding a general formula for the integrals of polynomials, but he was not concerned with any polynomials higher than the fourth degree.

In the late 11th century, Omar Khayyam wrote Discussions of the Difficulties in Euclid, a book about what he perceived as flaws in Euclid’s Elements especially the parallel postulate.

He was also the first to find the general geometric solution to cubic equations. He was also very influential in calendar reform.

In the 13th century, Nasir al-Din Tusi  (Nasireddin) made advances in spherical trigonometry.

He also wrote influential work on Euclid’s parallel postulate.

In the 15th century, Ghiyath al-Kashi computed the value of π to the 16th decimal place.

Kashi also had an algorithm for calculating nth roots, which was a special case of the methods given many centuries later by Ruffini and Horner.

Other achievements of Muslim mathematicians during this period include the addition of the decimal point notation to the Arabic numerals, the discovery of all the modern trigonometric notation besides the sine, al-Kindi’s introduction of cryptanalysis and frequency analysis, the development of analytic geometry by Ibn al-Haytham, the beginning of algebraic geometry by Omar Khayyam and the development of an algebraic notation by al-Qalasadi.

During the time of the Ottoman empire and the Safavid empire, from the 15th century, the development of Islamic mathematics stagnated. Why? What happened? This could be called the Arabic question, just as the problem of why China stopped her phenomenal growth and highly advanced development around the time our own Renaissance began could be called the China question. Are civilizations/cultures like plants? Do they have their own internal clocks?

Interest in mathematics in Medieval Europe was driven by concerns quite different from those of modern mathematicians.

People then believed that mathematics would provide the key to understanding the created order of nature, frequently justified by Plato’s Timaeus and the biblical passage (Book of Wisdom) that God had ordered all things in measure, and number, and weight.

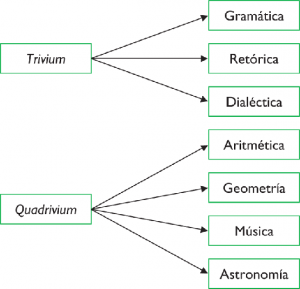
Boethius provided a place for mathematics in the curriculum in the 6th century when he used the term quadrivium to describe the study of arithmetic, geometry, astronomy, and music.

De institutione arithmetica was Boethius’ free translation from the Greek of Nicomachus’ Introduction to Arithmetic.

De institutione musica, also by Boethius, derived from Greek sources, especially from a series of excerpts of Euclid’s Elements.

These works were theoretical, rather than practical, and were the basis of mathematical study until the recovery of Greek and Arabic mathematical works.

European began to travel south to Spain and Italy by the twelfth century seeking scientific and philosophical Arab texts, including al-Kharizmi’s Compendius Boon on Calculation by Completeion and Balancing, which was then translated into Latin by Robert of Chester.

The complete text of Euclid’s Elements was translated in various versions by Adelard of Bath, Herman of Carinthia and Gerard of Cremona.

The new translations aroused a new interest in mathematics.

Leonardo Pisano Bigollo (1170-1250), better known as Fibonacci, writing in the Liber Abaci (Book of the Abacus), produced the first significant mathematics in Europe since the time of Eratosthenes, a gap of more than a thousand years.

Fibonacci’s book introduced Hindu/Arabic numerals (modus Indorum, method of the Indians) to Europe, and discussed many other mathematical problems.

The 14th century saw the development of new mathematical concepts to investigate a wide range of problems.

One important contribution was development of mathematics of local motion.

Thomas Bradwardine proposed that speed (V) increases in arithmetic proportion as the ratio of force (F) to resistance (R) increases in geometric proportion.

Bradwardine expressed this by a series of specific examples, but although the logarithm had not yet been conceived, we can express his conclusion anachronistically by writing: V = log (F/R).

Bradwardine’s analysis is an example of transferring a mathematical technique used by al-Kindi and Arnald of Villanova to quantify the nature of compound medicines to a different physical problem.

William Heytesbury (circa 1313 – 1372/1373), one of the 14th-century Oxford calculators, lacking differential calculus and the concept of limits, proposed to measure instantaneous speed “by the path that would be described by [a body] if… it were moved uniformly at the same degree of speed with which it is moved in that given instant.”

Heytesbury mathematically determined the distance covered by a body undergoing uniformly accelerated motion (today solved by integration), stating that “a moving body uniformly acquiring or losing that increment [of speed] will traverse in some given time a [distance] completely equal to that which it would traverse if it were moving continuously through the same time with the mean degree [of speed]“.

Nicole Oresme at the Université de Paris and the Italian Giovanni di Casali independently provided graphical demonstrations of this relationship, asserting that the area under the line depicting the constant acceleration, represented the total distance traveled.

Later, commenting on Euclid’s Elements, Oresme made a more detailed general analysis in which he demonstrated that a body will acquire in each successive increment of time an increment of any quality that increases as the odd numbers.

Since Euclid had demonstrated the sum of the odd numbers are the square numbers, the total quality acquired by the body increases as the square of the time.

During the Renaissance, the development of mathematics and of accounting were intertwined were studied at the same time.

While there is no direct relationship between algebra and accounting, the teaching of the subjects and the books published often intended for the children of merchants who were sent to reckoning schools in Flanders or Germany or abacus schools (known as abbaco in Italy), where they learned the skills useful for trade and commerce.

In the abacus schools principles of reckoning were taught in the vernacular languages rather than in Latin.

There is probably no need for algebra in performing bookkeeping operations, but for complex bartering operations or the calculation of compound interest, a basic knowledge of arithmetic was mandatory and knowledge of algebra was very useful.

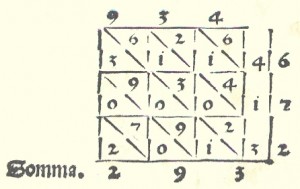
The Summa de Arithmetica, Geometria, Proportioni et Proportionalità of Luca Pacioli was first printed and published in Venicein 1494,

The Summa included a 27-page treatise on bookkeeping “Particularis de Computis et Scripturis” (Details of Calculation and Recording). and was written primarily for, and sold mainly to, merchants who used the book as a reference text, as a source of pleasure from the mathematical puzzles it contained, and to aid the education of their sons.

Pacioli introduced symbols for plus and minus for the first time in the Summa, symbols that became standard notation in Italian Renaissance mathematics.

The Summa Arithmetica was also the first known book printed in Italy to contain algebra.

It is important to note that Pacioli himself had borrowed much of the work of Piero della Francesca whom he plagiarized.

Long passages in the book are merely a restating of della Francesca’s work.

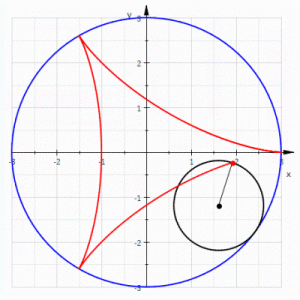
In Italy, during the first half of the 16th century, Scipione del Ferro and Niccolò Fontana Tartaglia discovered solutions for cubic equations. (“Tartaglia” means “the stammerer,” because Fontana was injured in a battle against an invading French army which caused his speech defect.)

Gerolamo Cardano published the cubic equations in his 1545 book Ars Magna together with a solution for the quartic equations discovered by his student Lodovico Ferraro.

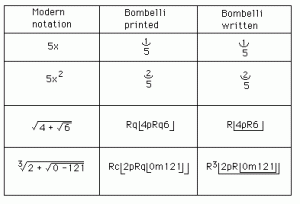
In 1572 Rafael Bombelli published his L’Algebra in which he showed how to deal with the imaginary quantities that could appear in Cardano’s formula for solving cubic equations.

De Thiende (‘the art of tenths’), by Simon Stevin, first published in Dutch in 1585, contained the first systematic treatment of decimal notation, which influenced all later work on the real number system.

Stevin is credited with the invention of the decimal point, although, as we have seen, place value notation had long been practiced by the Chinese, Indians, Arabs and others.

Trigonometry grew to be a major branch of mathematics because large areas of the world needed to be accurately mapped and there were many more ships at sea now.

Bartholomaeus Pitiscus invented the word “trigonometry,” publishing his Trigonometria in 1595.

Regiomontanus’s table of sines and cosines was published in 1533.

During the Renaissance the desire of artists to represent the natural world realistically, together with the rediscovered philosophy of the Greeks, led artists to study mathematics and mathematicians to study art.

Artists were also the engineers and architects of that time, and so had need of mathematics in any case.

The art of painting in perspective, and the developments in geometry that involved, were studied intensely.

The Seventeenth Century was an age of science in Europe.

Robert Boyle began his experiments during this period and Galileo Galilei observed the moons of Jupiter in orbit about that planet, using a telescope based on a toy imported from Holland.

Tycho Brahe had gathered an enormous quantity of mathematical data describing the positions of the planets in the sky.

Johannes Kepler, Brahe’s assistant, was also, to put it mildly, very interested in planetary motion.

The invention of logarithms by John Napier and Jost Bürgi made Kepler’s calculations a lot easier.

Kepler succeeded in formulating mathematical laws of planetary motion.

The analytic geometry of René Descartes (1596–1650) allowed those orbits to be plotted on a graph, as Cartesian coordinates.

Simon Stevin, as we have mentioned, created the basis for modern decimal notation capable of describing all numbers, whether rational or irrational.

Isaac Newton discovered the laws of physics explaining Kepler’s laws and brought together the concepts now known as infinitesimal calculus.

In one of those congruencies that happen now and again in human history, Newton and Leibniz independently invented calculus at about the same time.

Probably most musicians have had the experience of writing something, putting it aside, and then hearing it later on the radio, the work of someone else.

No one copied anyone.

The idea was ready to be born and it was born in two places at once.

Consider the countercultural movement that happened in San Francisco from 1965 to 1970.

That movement, that questioning of authority, occurred all over the world at about the same time.

The Red Guards in China were a part of that phenomenon, even though it would have disgusted them to realize that.

It was the Chinese youth’s mission to do away with the old and to submit all received ideas to the cold light of reëxamination.

There were excesses as there often are in such profound and universal movements.

One has only to contemplate the Reign of Terror in the French Revolution to see that lawlessness can very quickly lead to fascism.

Gottfried Wilhelm Leibniz, who is arguably the most important mathematician of the 17th century, developed this calculus that he and Newton had invented and also much of the calculus notation still in use today.

In addition to the application of mathematics to the studies of the heavens, applied mathematics began to expand into new areas, as signaled in  the correspondence of Pierre de Fermat and Blaise Pascal.

Pascal and Fermat set the groundwork for the investigations of probability theory and the corresponding rules of combinatorics in their discussions over a game of gambling.

Pascal, with his wager, attempted to use the newly developing probability theory to argue for a life devoted to religion, on the grounds that even if the probability of success was small, the rewards were infinite.

In some sense, this foreshadowed the development of utility theory in the 18th–19th century.

Leonhard Euler was probably the most influential mathematician of the 18th century.

His contributions range from founding the study of graph theory with the Seven Bridges of Königsberg problem to standardizing many modern mathematical terms and notations.

Euler named the square root of minus 1 with the symbol i, and he popularized the use of the Greek letter  to stand for the ratio of a circle’s circumference to its diameter.

He made numerous contributions to the study of topology, graph theory, calculus, combinatorics, and complex analysis, and a multitude of theorems and notations are named for him.

Joseph Louis Lagrange, who did pioneering work in number theory, algebra, differential calculus, and the calculus of variations, and Laplace who, in the age of Napoléon did important work on the foundations of celestial mechanics and on statistics, were other important eighteenth century mathemaicians.

In the 19th century mathematics became increasingly abstract.

Carl Friedrich Gauss (1777–1855), setting aside his many contributions to pure mathematics, did revolutionary work on functions of complex variables, in geometry and on the convergence of series.

Gauss gave the first satisfactory proofs of the fundamental theorem of algebra and of the quadratic reciprocity law.

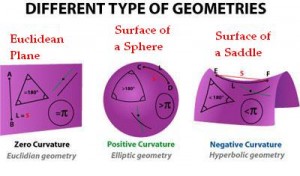
The twentieth century saw the development of the two forms of non Euclidean geometry.

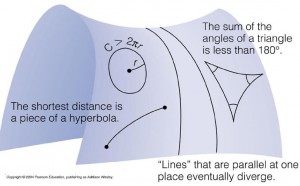
The Russian mathematician Nikolai Ivanovich Lobachevsky and his rival, the Hungarian mathematician János Bolyai, independently defined and studied hyperbolic geometry where uniqueness of parallels no longer holds.

In this geometry the sum of angles in a triangle add up to less than 180°.

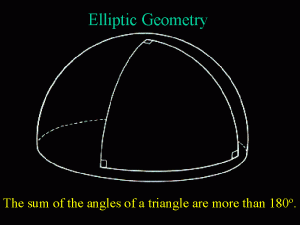
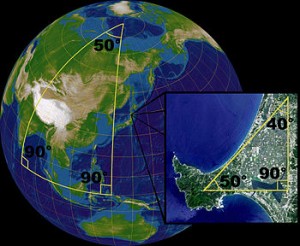
Elliptic geometry was developed later in the 19th century by the German mathematician Bernhard Riemann.

In elliptic geometry, there is no parallel and the angles in a triangle add up to more than 180°.

Riemann also developed Riemannian geometry which unifies and vastly generalizes the three types of geometry, and he defined the concept of a manifold, which generalizes the ideas of curves and surfaces.

Hermann Grassmann in Germany gave a first version of vector spaces, and William Rowan Hamilton  in Ireland developed noncommutative algebra.

The British mathematician George Boole devised an algebra that soon evolved into what is now called Boolean algebra, in which the only numbers were 0 and 1.

Boolean algebra is the starting point of mathematical logic and has important applications in computer science.

Agustin-Louis Cauchy, Bernhard Riemann and Karl Weierstrass reformulated the calculus in a more rigorous fashion.

Niels Henrik Abel, a Norwegian, and Évariste Galois, from France, proved that there is no general algebraic method for solving polynomial equations of degree greater than four (the Abel-Ruffini theorem).

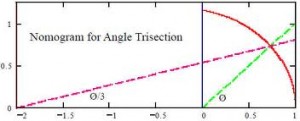
Other 19th-century mathematicians utilized this in their proofs that straightedge and compass alone are not sufficient to trisect an arbitrary angle.

Mathematicians had vainly attempted to solve all of these problems since the time of the ancient Greeks.

The limitation of three dimensions in geometry, however, was surpassed in the 19th century through considerations of parameter space and hypercomplex numbers.

The Abel and Galois investigations into the solutions of various polynomial equations laid the groundwork for further developments of group theory and the associated fields of abstract algebra.

Twentieth century physicists and other scientists have seen group theory as the ideal way to study symmetry.

In the later 19th century, Georg Cantor established the first foundations of set theory, which enabled the rigorous treatment of the notion of infinity and has become the common language of nearly all mathematics.

Cantor’s set theory, and the rise of mathematical logic in the hands of Peano, L.E.J. Brouwer, David Hilbert, Bertrand Russell and Alfred North Whitehead  initiated a long running debate on the foundations of mathematics.

A number of national mathematical societies were founded in the nineteenth century: the London Mathematical Society in 1865; the Société Mathématique de France in 1872; the Circolo Matematico di Palermo in 1884; the Edinburgh Mathematical Society in 1883; and the American Mathematical Society in 1888.

The first international, special-interest society, the Quaternion Society was formed in 1899, in the context of a vector controversy.

The 20th century saw mathematics become a major profession.

Every year, thousands of new Ph.D.s in mathematics were awarded, and jobs were available in both teaching and industry.

An effort to catalogue the areas and applications of mathematics was undertaken in Klein’s encyclopedia.

In a 1900 speech to the International Congress of Mathematicians, David Hilbert set out a list of 23 unsolved problems in mathematics.

These problems, spanning many areas of mathematics, formed a central focus for much of 20th-century mathematics.

Today, 10 of the 23 problems have been solved, 7 are partially solved, and 2 are still open. The remaining 4 are too loosely formulated to be stated as solved or not.

In 1976, Wolfgang Haken and Kenneth Appel used a computer to prove the four color theorem.

Andrew Wiles, building on the work of others, proved Fermat’s Last Theorem in 1995.

“Paul Cohen was one of the most brilliant mathematicians of the 20th century,” said Princeton Math Professor Peter Sarnak, who received his doctorate from Stanford in 1980 under Cohen’s direction.

Paul Cohen and Kurt Gödel proved that the continuum hypothesis is independent of (could neither be proved nor disproved from) the standard axioms of set theory.

In 1998 Thomas Callister Hales proved the Kepler conjecture.

Mathematical collaborations of unprecedented size and scope were happening.

The classification of finite simple groups (also called the “enormous theorem”), whose proof between 1955 and 1983 required 500-odd journal articles by about 100 authors, fills tens of thousands of pages.

A group of French mathematicians, including Jean Dieudonné and André Weil, publishing under the pseudonym “Nicolas Bourbaki,”   attempted to exposit all of known mathematics as a coherent rigorous whole.

The resulting several dozen volumes has had a controversial influence on mathematical education.

Differential geometry came into its own when Einstein used it in general relativity.

Entire new areas of mathematics such as mathematical logic, topology and John von Neumann’s game theory changed the kinds of questions that could be answered by mathematical methods.

In 2000, the Clay Mathematics Institute announced the seven Millenium Prize Problems.

And in 2003 the Poincaré conjecture was solved by Grigori Perelman (who declined to accept an award on this point).

Most mathematical journals now have online versions as well as print versions, and many online-only journals are launched.

There is an increasing drive towards open access publishing first popularized by the arXiv.

Sam Andrew

________________________________